banner



Home  ›  What Is The Purpose Of Drawing Electric Field Lines

What Is The Purpose Of Drawing Electric Field Lines

Written By Wednesday, March 30, 2022 Add Comment Edit

Electrical Charges and Fields

34 Electric Field Lines

Learning Objectives

Past the end of this section, y'all will be able to:

  • Explain the purpose of an electric field diagram
  • Describe the relationship between a vector diagram and a field line diagram
  • Explain the rules for creating a field diagram and why these rules make physical sense
  • Sketch the field of an capricious source accuse

Now that we have some experience calculating electric fields, let'south endeavour to gain some insight into the geometry of electric fields. Equally mentioned earlier, our model is that the charge on an object (the source charge) alters space in the region around information technology in such a mode that when another charged object (the test charge) is placed in that region of space, that test charge experiences an electric force. The concept of electrical field line s, and of electric field line diagrams, enables us to visualize the way in which the space is altered, assuasive united states to visualize the field. The purpose of this department is to enable you to create sketches of this geometry, so we will listing the specific steps and rules involved in creating an accurate and useful sketch of an electric field.

It is important to think that electrical fields are 3-dimensional. Although in this volume we include some pseudo-three-dimensional images, several of the diagrams that you'll see (both here, and in subsequent chapters) will be 2-dimensional projections, or cantankerous-sections. E'er keep in mind that in fact, you're looking at a three-dimensional phenomenon.

Our starting betoken is the physical fact that the electric field of the source charge causes a exam charge in that field to experience a forcefulness. By definition, electrical field vectors point in the aforementioned direction equally the electric force that a (hypothetical) positive test accuse would experience, if placed in the field ((Figure))

The electric field of a positive signal charge. A large number of field vectors are shown. Similar all vector arrows, the length of each vector is proportional to the magnitude of the field at each point. (a) Field in two dimensions; (b) field in three dimensions.

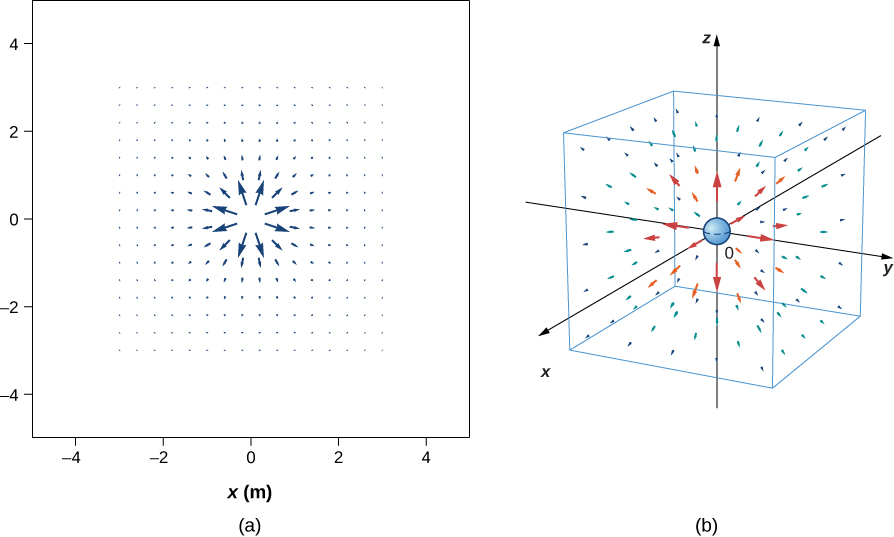
The electric field is shown as arrows at test points on a grid. In figure a, the field is shown in the x y plane, with x and y measured in meters and ranging from -4 meters to 4 meters. The arrows point away from the origin, and are largest near the origin, decreasing with distance from the origin. In figure b, a three dimensional vector field is shown. The charge is at the center and, again, the arrows are largest near the origin, decreasing with distance from the origin.

We've plotted many field vectors in the figure, which are distributed uniformly around the source charge. Since the electric field is a vector, the arrows that we draw correspond at every point in space to both the magnitude and the management of the field at that point. Every bit always, the length of the pointer that we draw corresponds to the magnitude of the field vector at that signal. For a betoken source charge, the length decreases by the square of the distance from the source charge. In addition, the management of the field vector is radially away from the source charge, because the direction of the electrical field is defined by the direction of the force that a positive test charge would experience in that field. (Again, proceed in heed that the bodily field is iii-dimensional; there are likewise field lines pointing out of and into the page.)

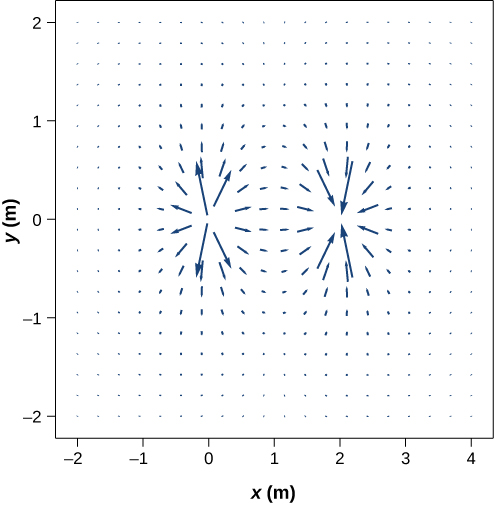
This diagram is correct, but information technology becomes less useful as the source charge distribution becomes more than complicated. For case, consider the vector field diagram of a dipole ((Figure)).

The vector field of a dipole. Even with just two identical charges, the vector field diagram becomes hard to understand.

A vector plot of the electric field due to two sources. The sources are not shown. The field is represented by arrows in an x y graph. Both x and y are in meters and both scales are from -2 meters to 4 meters. Near the origin, the arrows are long and point away from it. Near the point at coordinates 2, 0 the arrows are long and point toward the point. The arrows get smaller as we move farther from those two location and point in intermediate directions.

There is a more useful mode to present the same information. Rather than drawing a large number of increasingly smaller vector arrows, we instead connect all of them together, forming continuous lines and curves, as shown in (Figure).

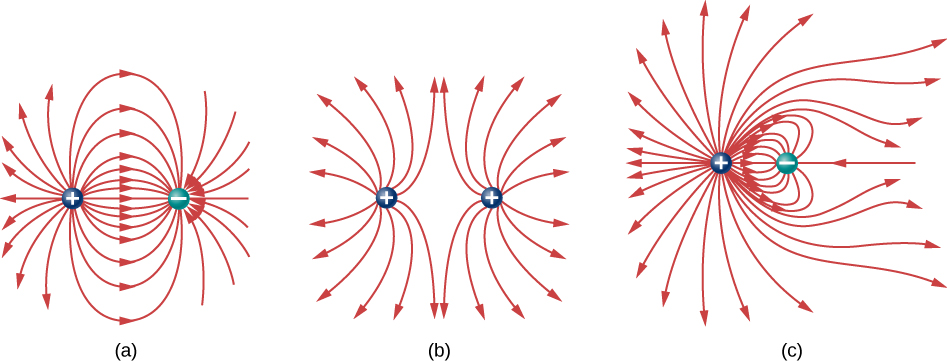
(a) The electric field line diagram of a positive point charge. (b) The field line diagram of a dipole. In both diagrams, the magnitude of the field is indicated by the field line density. The field vectors (not shown hither) are everywhere tangent to the field lines.

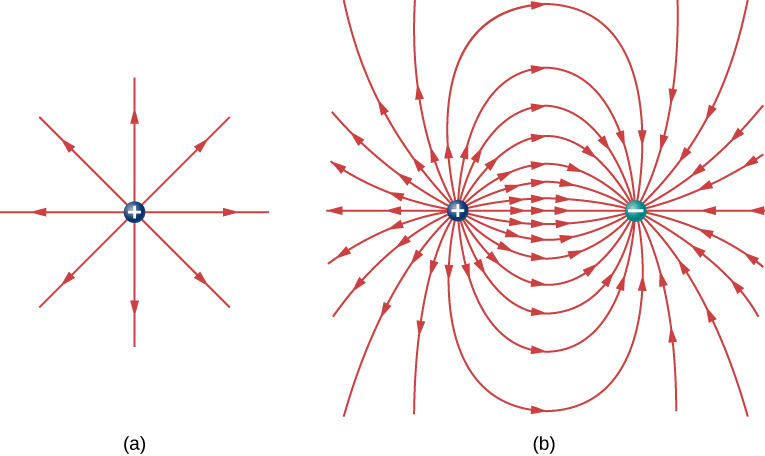
In part a, electric field lines emanating from a positive charge are shown as straight arrows radiating out from the charge in all directions. In part b, a pair of charges is shown, with one positive and the other negative. The field lines are represented by curved arrows. The arrows start from the positive charge, radiating outward but curving to end at the negative charge. The outer field lines extend beyond the drawing region, but follow the same behavior as those that are within the drawing area.

Although it may not be obvious at first glance, these field diagrams convey the same information near the electric field as do the vector diagrams. Start, the direction of the field at every indicate is simply the direction of the field vector at that same point. In other words, at any signal in infinite, the field vector at each signal is tangent to the field line at that same betoken. The arrowhead placed on a field line indicates its direction.

As for the magnitude of the field, that is indicated by the field line density—that is, the number of field lines per unit surface area passing through a small cross-sectional expanse perpendicular to the electric field. This field line density is drawn to be proportional to the magnitude of the field at that cross-section. As a result, if the field lines are close together (that is, the field line density is greater), this indicates that the magnitude of the field is big at that point. If the field lines are far apart at the cross-section, this indicates the magnitude of the field is modest. (Figure) shows the thought.

Electrical field lines passing through imaginary areas. Since the number of lines passing through each area is the same, but the areas themselves are different, the field line density is different. This indicates unlike magnitudes of the electric field at these points.

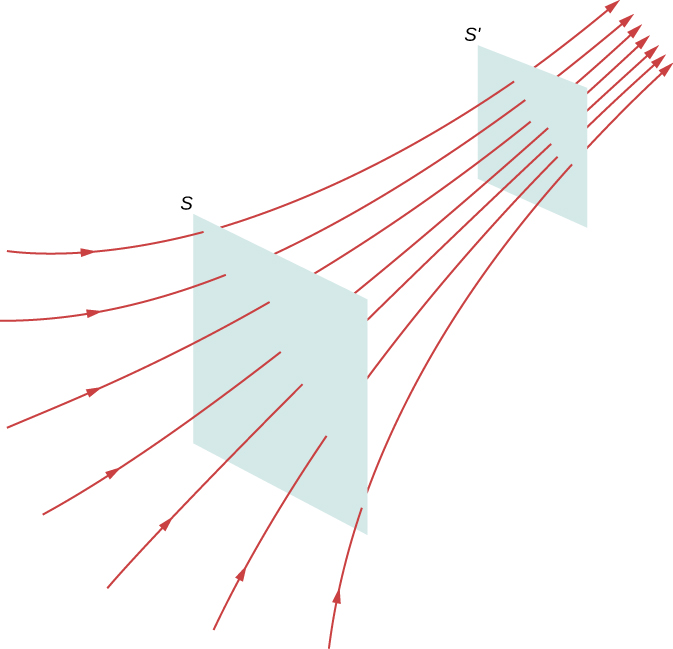
Seven electric field lines are shown, generally going from bottom left to top right. The field lines get closer together toward the top. Two square areas, perpendicular to the field lines, are shaded. All of the field lines pass through each shaded area. The area toward the top is smaller than the area toward the bottom.

In (Figure), the aforementioned number of field lines passes through both surfaces (S and S\text{′}\right), but the surface S is larger than surface S\text{′}. Therefore, the density of field lines (number of lines per unit area) is larger at the location of S\text{′}, indicating that the electric field is stronger at the location of S\text{′} than at S. The rules for creating an electric field diagram are equally follows.

Problem-Solving Strategy: Drawing Electric Field Lines

  1. Electrical field lines either originate on positive charges or come in from infinity, and either terminate on negative charges or extend out to infinity.
  2. The number of field lines originating or terminating at a charge is proportional to the magnitude of that charge. A charge of twoq will have twice every bit many lines every bit a charge of q.
  3. At every point in space, the field vector at that point is tangent to the field line at that same point.
  4. The field line density at any signal in infinite is proportional to (and therefore is representative of) the magnitude of the field at that point in space.
  5. Field lines can never cantankerous. Since a field line represents the direction of the field at a given point, if two field lines crossed at some point, that would imply that the electric field was pointing in two different directions at a unmarried indicate. This in plow would suggest that the (net) force on a exam charge placed at that indicate would point in 2 unlike directions. Since this is obviously impossible, it follows that field lines must never cross.

Ever keep in mind that field lines serve only as a convenient way to visualize the electrical field; they are not physical entities. Although the direction and relative intensity of the electric field can be deduced from a set of field lines, the lines can also be misleading. For example, the field lines drawn to stand for the electrical field in a region must, by necessity, be discrete. However, the actual electric field in that region exists at every signal in space.

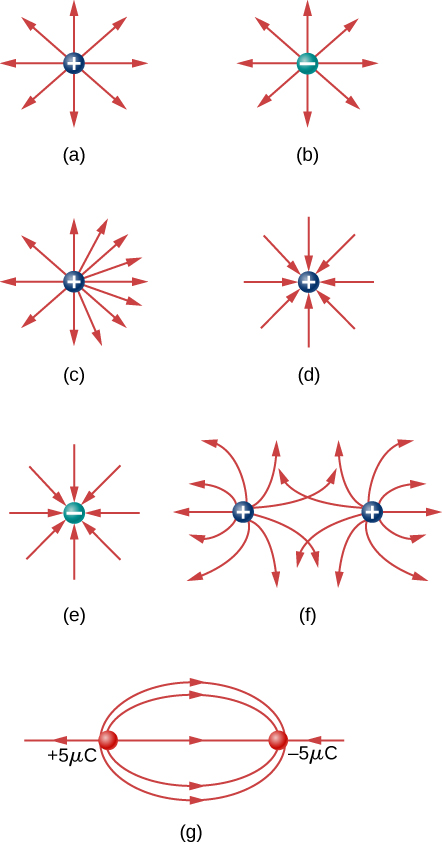
Field lines for three groups of detached charges are shown in (Figure). Since the charges in parts (a) and (b) have the same magnitude, the aforementioned number of field lines are shown starting from or terminating on each charge. In (c), nevertheless, we describe iii times as many field lines leaving the \text{+}3q charge as entering the \text{−}q. The field lines that do not stop at \text{−}q emanate outward from the accuse configuration, to infinity.

Iii typical electrical field diagrams. (a) A dipole. (b) Two identical charges. (c) Ii charges with opposite signs and unlike magnitudes. Tin y'all tell from the diagram which charge has the larger magnitude?

Three pairs of charges and their field lines are shown. The charge on the left is positive in each case. In part a, the charge on the right is negative. The field lines are represented by curved arrows starting at the positive charge on the left, curving toward and terminating at the negative charge on the right. Between the charges, the field lines are dense. In part b, the charge on the right is positive. The field lines represented by curved arrows start at each of the positive charges and diverge outward. Between the charges, the field lines are less dense, and there is a black region midway between the charges. In part c, the charge on the right is negative. The field lines start at the positive charge. Some of the lines, those that start closest to the negative charge, curve toward the negative charge and terminate there. Lines that start further from the negative charge curve toward it but then diverge outward. There is an area with very low density of lines to the right of the pair of charges.

The power to construct an accurate electric field diagram is an important, useful skill; information technology makes it much easier to approximate, predict, and therefore calculate the electrical field of a source charge. The best way to develop this skill is with software that allows yous to place source charges then will draw the cyberspace field upon request. Nosotros strongly urge you lot to search the Internet for a program. Once you've found 1 you similar, run several simulations to go the essential ideas of field diagram structure. And so practice cartoon field diagrams, and checking your predictions with the reckoner-fatigued diagrams.

Summary

  • Electric field diagrams assist in visualizing the field of a source charge.
  • The magnitude of the field is proportional to the field line density.
  • Field vectors are everywhere tangent to field lines.

Conceptual Questions

If a point charge is released from residual in a compatible electric field, will information technology follow a field line? Will information technology do and so if the electric field is not uniform?

yes; no

Under what conditions, if any, will the trajectory of a charged particle not follow a field line?

How would y'all experimentally distinguish an electrical field from a gravitational field?

At the surface of Earth, the gravitational field is ever directed in toward Earth'south eye. An electric field could movement a charged particle in a different direction than toward the heart of Earth. This would indicate an electric field is present.

A representation of an electric field shows ten field lines perpendicular to a foursquare plate. How many field lines should pass perpendicularly through the plate to depict a field with twice the magnitude?

What is the ratio of the number of electric field lines leaving a charge 10q and a charge q?

10

Bug

Which of the following electric field lines are wrong for signal charges? Explain why.

Figure a shows field lines pointing away from a positive charge. The lines are uniformly distributed around the charge. Figure b shows field lines pointing away from a negative charge. The lines are uniformly distributed around the charge. Figure c shows field lines pointing away from a positive charge. The lines are denser on the right side of the charge than on the left. Figure d shows field lines pointing toward a positive charge. The lines are uniformly distributed around the charge. Figure e shows field lines pointing toward a negative charge. The lines are uniformly distributed around the charge. Figure f shows two positive charges. Field lines start at each positive charge and point away from each. The lines are uniformly distributed at the charges and bend away from the midline. Some lines intersect each other. Figure g shows a positive 5 micro Coulomb charge and a negative micro Coulomb charge. Several field lines are shown. Long the line connecting the charges is a field line that points away from the positive charge and toward the negative one. Another field line forms an ellipse that starts at the positive charge and ends at the negative charge. Another field line also forms an ellipse that points away from the positive and ends at the negative charge but appears to envelop the charges rather than start and end at the charges.

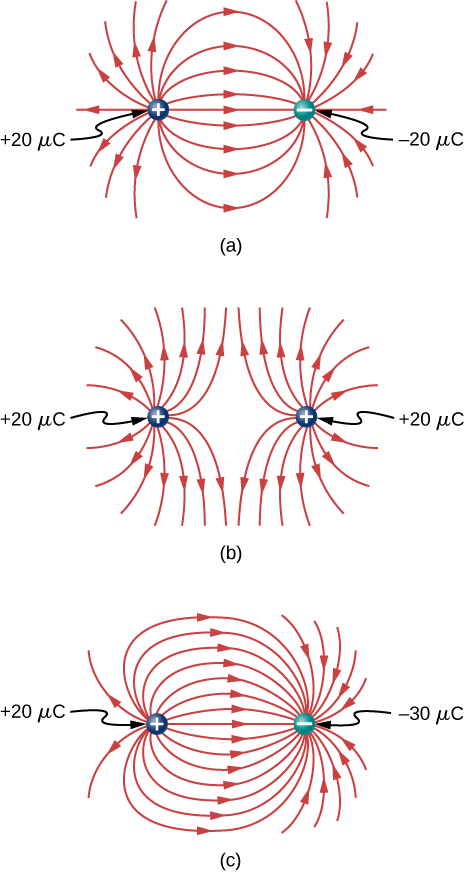
In this practise, y'all volition practice cartoon electric field lines. Make sure you stand for both the magnitude and management of the electric field fairly. Note that the number of lines into or out of charges is proportional to the charges.

(a) Describe the electric field lines map for two charges \text{+}20\phantom{\rule{0.2em}{0ex}}\mu \text{C} and -20\phantom{\rule{0.2em}{0ex}}\mu \text{C} situated v cm from each other.

(b) Draw the electrical field lines map for 2 charges \text{+}20\phantom{\rule{0.2em}{0ex}}\mu \text{C} and \text{+}20\phantom{\rule{0.2em}{0ex}}\mu \text{C} situated 5 cm from each other.

(c) Describe the electric field lines map for ii charges \text{+}20\phantom{\rule{0.2em}{0ex}}\mu \text{C} and -30\phantom{\rule{0.2em}{0ex}}\mu \text{C} situated v cm from each other.

Figure a shows a positive 20 micro Coulomb charge on the left, a negative 20 micro Coulomb charge on the right, and the field lines due to the charges. The field lines come out of the positive charge and converge coming into the negative charge. The outer field lines extend beyond the drawing area and so we see them bending to the right, toward the negative charge, but only see part of the line. The density of lines coming out of the positive is the same as the density going into the negative. Figure b shows a positive 20 micro Coulomb charge on the left, a positive 20 micro Coulomb charge on the right, and the field lines due to the charges. The field lines come out of the positive charges and diverge, bending away from the far charge. The density of lines is the same near each of the charges. Figure c shows a positive 20 micro Coulomb charge on the left, a negative 30 micro Coulomb charge on the right, and the field lines due to the charges. The field lines come out of the positive charge. More lines go into the negative 20 micro Coulomb charge than come out of the positive 20 micro Coulomb charge. All of the lines coming out of the positive charge terminate at the negative, while the outer lines going into the negative start at infinity.

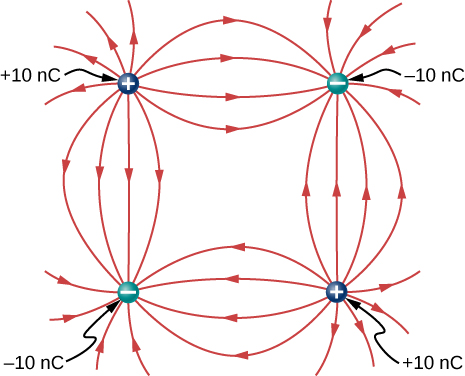
Two charges of equal magnitude merely opposite sign make up an electric dipole. A quadrupole consists of two electric dipoles are placed anti-parallel at ii edges of a square as shown.

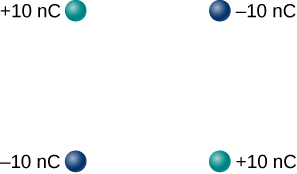
Four charges are shown at the corners of a square. At the top left is positive 10 nano Coulombs. At the top right is negative 10 nano Coulombs. At the bottom left is negative 10 nano Coulombs. At the bottom right is positive 10 nano Coulombs.

Describe the electric field of the charge distribution.

Four charges are shown at the corners of a square. At the top left is positive 10 nano Coulombs. At the top right is negative 10 nano Coulombs. At the bottom left is negative 10 nano Coulombs. At the bottom right is positive 10 nano Coulombs. The field lines are also shown. They come out of the positive charges and curve toward and end at the negative charges. The lowest density is near the center of the square.

Suppose the electric field of an isolated point charge decreased with distance as 1\text{/}{r}^{2+\delta } rather than as 1\text{/}{r}^{2}. Show that it is then impossible to describe continous field lines then that their number per unit area is proportional to Due east.

Glossary

field line
smooth, usually curved line that indicates the direction of the electric field
field line density
number of field lines per square meter passing through an imaginary area; its purpose is to indicate the field strength at dissimilar points in space

Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/electric-field-lines/

Posted by: blancharddeve1941.blogspot.com

0 Response to "What Is The Purpose Of Drawing Electric Field Lines"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel